The first references to a natural interest rates appear to relate to the work of Johan Gustaf Knut Wicksell (1851 – 1926), a Swedish economist. Trained as a mathematician he did attend lectures by the founder of the Austrian school, the economist Carl Menger, in Vienna.

Early involvement in constitutional economics

Wicksell made early contributions to the foundations of constitutional economics. His work on income distribution concluded that even in a totally free economy wealth could not be equalized since wealth created by growth would be distributed to those who had wealth in the first place. Based on his own marginal allocation theory he considered the role for government intervention to be to improve national welfare. He established a foundation for constitutional political economy in 1896 with work on fiscal theory in which he drew attention to the significance of the rules within which choices are made by political agents. He emphasized that efforts at reform required changes in the rules for making decisions rather than trying to influence the behaviour of the actors. This observation was elaborated in the works of James Buchanan (1919 – 2013) and Gordon Tullock (1922 – 2014) concerning public choice theory

Natural interest rate

No unique natural interest rate According to the feasible rate of return on an investment there will be an optimised natural interest rate that results in an acceptable trade-off between the amount borrowed, the amount to be paid back and the return on investment. On the part of an individual lender there will also be an optimised natural interest rate that results in an acceptable trade-off between the amount lent, the amount to be paid back and other lending options (opportunity cost). Any transaction will be close to these optimised natural interest rates. In each case investors and lenders face different states of the factors that need to be taken into account leading to a wide spread in what would be considered to be natural interest rates. For example different sectors have a very large range of returns on investment varying from as low as -10% to well over 60% and the interest rates considered to be payable will vary across this range according to available information and perceived risk. Moving companies (investors) and lenders away from their desired transactionable interest rates which are intimately related to microeconomic specifics, only leads to sub-optimal transactions and imposes constraints on the flow of funds into desirable investments.

Wicksell coined the term "natural rate of interest" as that interest rate compatible with a stable price level. The implications were that if interest rates fell short of the natural rate, inflation would be likely to arise; if the interest rate exceeded the natural rate, this will tend to produce deflation. An interest rate that coincides with the natural rate was considered to ensure equilibrium in the commodity market and produce price level stability.

Returns on investment and interest rates

However, Wicksell referred to the macroeconomic situation and an "average interest rate". However, in reality there is no such thing as a generally applicable or unique natural interest rate. This is because what constitutes a stabilising interest rate that facilitates investment depends upon the specific feasible potential return on investment associated with each individual company within each economic sector. Since each company has a different opportunities and capabilities of managing investments to secure what is a feasible return, there is a myriad of natural interest rates each representing an "actionable" level at which it is worth investing. Any national level "interest rate" established as an average of all actionable natural interest rates, or set by the state, cannot be an optimal interest rate simply because of the different conditions and investment potential of each company in the economy; there will be winners and losers associated with any particular rate. However, applying this theoretical "average" it is considered that Wicksell's concept of the natural interest rate contributed to the quantity theory of money (QTM) in the sense that the raising of money volumes, by lowering interest rates, would lead to price rises being an inevitable long run outcome. The driving force for this is, theoretically, the growth in investment associated with low interest rates generating demand and employment.

When is long run, long run?

In 2008 quantitative easing was introduced and interest rates lowered and after almost a decade the increased money supply has not resulted in either increased investment in production and service activities and prices have not risen appreciably. Therefore the QTM and Milton Friedman's claim of long term price rises has not been born out in practice.

Why is the QTM model wrong?

The QTM is variously described in terms of equations. For example the following relationship is a shorthand description of the theory:

M. V_T = P_T.T ..... (i)
Where:
M is the total amount of money in circulation;
V_T is the velocity of circulation or the average frequency across all transactions where money is spent.
P_T is the price level associated with transactions in the period under consideration;
T is an index of real value of aggregate transactions.

With the development of national accounts this equation was modified to:

M.V = P.Q ..... (ii)
Where:

M is the total amount of money in circulation;
V is the velocity of circulation or the average frequency across all transactions in final expenditures.
P is the price level associated with transactions in the period under consideration;
Q is an index of the real value of final expenditures.

The economists Marshall, Pigou & Keynes, all associated with Cambridge University, reasoned that the demand for money was more significant than the supply, in that a certain proportion of nominal income (designated as k in the short run) is not be used for transactions but it will be saved or held as cash. So the equation is modified as follows:

M = k . P. Y ..... (iii)

Where: P is the price level
Y real income.

or:
M/k = P . Y ..... (iv)

These economists also considered wealth to have some influence but for simplicity's sake, unfortunately wealth is often omitted from the equation.

However, the Cambridge equation shows the savings inserted as a veriable in a product (k.P.Y) whe the logic shouldbe that savings are not circulating and therefore are separate from P.V so the relationship of k + P.V. Therefore the equation should have been setout as:

M = k + P. Y ..... (v)

Where: P is the price level
Y real income.

or:
M - k = P . Y ..... (vi)

The last decade has shown that this version of the QTM is more realistic.

Adding wealth in the form of assets

In the shadow of the evidence of a decade of quantitative easing (QE) it is worth augmenting this modified Cambridge equation by adding in the effect of the flow of monetary expansion into assets. This is not a theoretical notion, it is what has happened. Thus designating "a" as asset holdings, that is money not circulating but invested in assets such as land, shares and stocks, the modified Cambridge equation can be made more "realistic" by writing it out as follows:

M = (a + k) + P. Y ..... (vii)

Where: P is the price level and Y real income.

or:

M - (a+k) = P . Y ..... (viii)

As has been observed as monetary volumes have been increased, the significant flow of these funds into assets has resulted in a reduction of the effective volume of funds flowing into the product P.Y which signifies that prices or real incomes or both have declined. Because asset prices have a collateral effect on some critical consumer prices such as land and real estate assets value rises causing rises in rents, then such price rises end up having a resultant impact of depressing real incomes.

The tables below show some scenarios based on the last version of this QTM equation i.e. equation (vi).

It is possible to generate hundreds of scenarios but the actual experience of the last decade is approximated in the first table below where asset holdings have risen more in proportion to cash holdings (which tend to be circulated) leading to a fall in real incomes. Because asset holdings are associated with a collateral impact on some prices such as rents, the condition of "full employment" can only be achieved if real incomes per capita are reduced. The table below shows an example of asset holdings rising using expanded monetary streams more than proportionally to the rise in cash holdings (which tend to circulate eventually) so a 100% rise in monetary volumes being associated with a fall in real incomes by 33.3%. In other words, with or without changes in unit prices real incomes will decline as a result of the diversion of monetary resources into assets because the availability of funds circulating in the real productive economy and paid to those employed declines. The only means of maintaining any given standard of living is to resort to credit/debt. The associated effect is a significant disparity in income distribution between the highest and the lowest paid.

M	δM	a	k	P.Y	δP.Y	δa
100	0%	20	20	60
200	100%	80	40	80	33.33%	400%

The tables below are other scenarios that have not occurred but they do indicate the effects of reducing assets holdings would be beneficial in terms of real incomes.

The table below shows an example of asset holdings rising in a fixed proportion to cash holdings using expanded monetary streams leading to a 100% rise in monetary volumes and zero rise in real incomes.

M	δM	a	k	P.Y	δP.Y	δa
100	0%	20	20	60
200	100%	40	40	120	100%	100%

The table below shows an example of asset holdings less in proportion to cash holdings that will be eventually circulated, leading to a rise in real incomes of 33.3% associated with monetary expansion of 100%.

M	δM	a	k	P.Y	δP.Y	δa
100	0%	20	20	60
200	100%	20	40	140	133.33%	0%

Work on the real incomes approach has demonstrated that inflation is generated by a single process. This is price setting by companies in response to input cost rises or opportunistic pricing associated with gaps in availability. Milton Friedman considered the sources of inflation to be related to the growth rate in money supplies and that the demand for money is related to its velocity and is directly related to nominal incomes and interest rates. Thus lower interest rates should raise the demand and velocity and feed through into nominal incomes. As we can see from the evidence this has not happened as a result of one of the largest examples of monetary expansion under low interest rates that has occurred; a case study in the disproof of the QTM concept. Friedman's assertions were challenged by Nicholas Kaldor and Friedman was never able to produce a convincing argument or evidence to support his position. To be fair, Wicksell also held on to the same long term theory but this was because he also held onto the same top down theory of a single average interest rate manipulated to control aggregate demand.

The QTM has been promoted as a basis for removing macroeconomic instability by adopting a low growth rate in money supply. However, since the 1970s the growth in financial intermediation and derivatives markets has made the quantification of appropriate money supplies virtually impossible so the interest rate was adopted as a policy instrument. The target of 2% annual inflation as a condition considered to represent price stability is bizarre given that this represents an 18% devaluation of the currency each decade. This is, therefore, a real incomes depreciation treadmill. This has also proven to be a useless policy instrument for stabilising real incomes, even at rock bottom interest rates, as the last decade has established.

So what is this natural interest rate?

The question remains as to why the Bank of England and the government continue with the highly destructive policy of Quantitative Easing when it is so evidently hollowing out the British economy. This policy remains in place as the country transitions towards a departure from the European Union which will result in yet additional instability and economic damage. It is self-evident that QE is prejudicing the majority of constituents through its continued exacerbation of the state of the economy and worsening state of income disparity. This process is supporting asset and wealth accumulation by a small interest group at the expense of real incomes growth of the majority. The real economy continues to decline as a result of this proactive policy of cash flow stripping. This constitutes a perverse process of economic sanctions directed against the interests of the people of this country and is an example of a blatant contravention to all principles of constitutional economics.

Centrally imposed un-natural interest rates

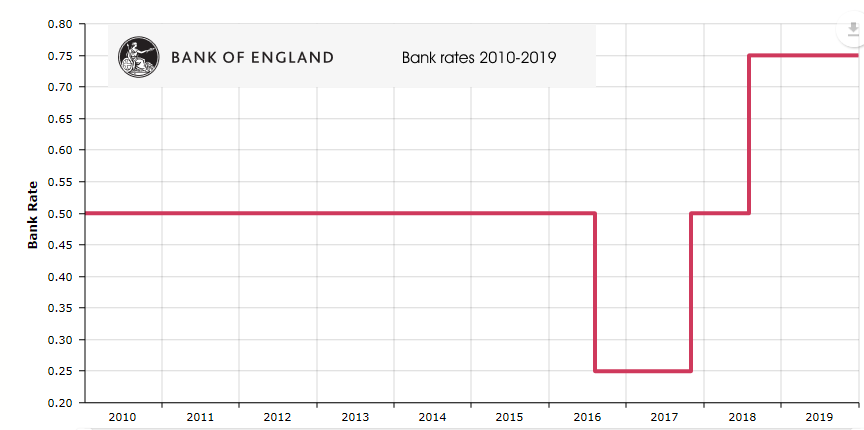In a situation where a company accumulates margins or savings it can make use of this money to change ways in which corporate processes are managed with a view to improving productivity and lowering costs. On the other hand this money could be lent to another company in return for interest. On the other hand, the return on investment in the company holding cash savings might be higher than the interest rate that people would be prepared to pay for borrowing that money.Therefore the interest rate at which this money would be transacted and used by a borrower will be the interest rate that exceeds the likely return on investment in the company of the monetary holdings. On the other hand where a company's potential returns on own investment are higher than the potential returns another company in need of funds could earn, then no transaction at that interest rate would occur. Therefore money would be sought from sources that do not have immediate means of investing funds such as personal savings where individuals would be prepared to lend money on the basis of an acceptable return. Such transactions being handled by third parties requiring a return for their service would end up paying the saver the net difference between the average return on a portfolio's investment less a commission. Under such circumstances it is evident that there are multiple natural interest rates each depending upon the source of savings and their access to investment opportunities or lending and/or borrowing opportunities. The most appropriate and beneficial interest rates will vary according to the specific partners in a transaction and for this reason there can be no single natural exchange rate since by fixing the interest rate, as an across-the-board standard rate, would make optimisation of rates based on negotiation according to lender and borrower circumstances impossible leading to significant constraints on the optimisation of investment activities. This is why centralised government or central bank intervention in interest rates is a very poor way of managing the economy by attempting change the levels of aggregate demand.

Clearly excessive interest rates kill off investment leading to future productivity constraints making it difficult to lower unit prices through advances in technology and technique just as ultra low interest rates have now been demonstrated to divert monetary expansion from achieving productivity enhancing investment to an "investment" in assets.

A linked article shows the impact of quantitative easing on monetary flows affecting real incomes: The outcome of quantitative easing on real incomes - summary note

---

¹ Hector McNeill is the Director of SEEL-Systems Engineering Economics Lab.